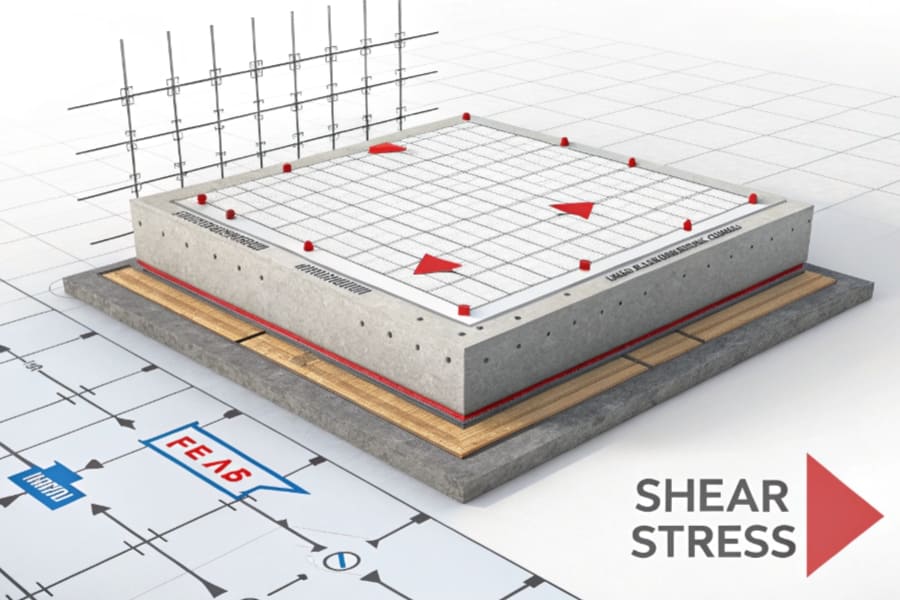
The shear modulus, also known as the modulus of rigidity, is a material property that defines how a material deforms under shear stress. It describes the material’s resistance to shape changes when a force is applied parallel to its surface. This concept is crucial for engineers working with materials exposed to shear forces, such as metals, plastics, and concrete.
The shear modulus is a critical material property that helps us understand how a material responds to shear stress. It is the ratio of shear stress to shear strain, providing insights into how much a material will deform when subjected to shear forces.
Shear modulus plays a pivotal role in the design of mechanical components. In this post, we will explore various aspects of shear modulus, compare it with other material properties like Young’s modulus and Poisson’s ratio, and examine its practical applications and how it is measured.
What is Shear Modulus vs Young’s Modulus?
When it comes to understanding material behavior under stress, both shear modulus and Young’s modulus are essential, yet they describe different types of stress and strain. But how do they differ?
Shear modulus measures a material’s resistance to shear stress, while Young’s modulus measures its resistance to elongation or compression under tensile or compressive forces.

The key difference between shear modulus and Young’s modulus lies in the type of stress they address. Young’s modulus is concerned with tensile or compressive stress, forces that pull or push on a material along its length. On the other hand, shear modulus deals with shear stress, where the material is deformed by forces acting parallel to its surface.
The relationship between shear modulus and Young’s modulus
Both shear modulus and Young’s modulus are useful for understanding material flexibility. The relationship between the two can often be linked through Poisson’s ratio for isotropic materials. For example, shear modulus can be derived from Young’s modulus if the Poisson’s ratio is known.
| Property | Young’s Modulus (E) | Shear Modulus (G) |
|---|---|---|
| Type of Stress | Tensile/Compressive | Shear |
| Material Behavior | Elongation/Compression | Twisting/Shearing |
| Formula | Calculate Formula(E) | Calculate Formula(G) |
Practical differences in applications
In engineering, Young’s modulus is used to predict how a material will behave under stretching or compression, such as in beams or columns. Shear modulus, in contrast, is more relevant when assessing materials subjected to twisting or shearing forces, like in shafts, gears, or structural components.
Are Shear Strength and Shear Modulus the Same?
Though the terms “shear strength” and “shear modulus” sound similar, they refer to very different material properties. Let’s explore how they differ.
Shear strength refers to the maximum stress a material can withstand before failure, while shear modulus measures how much a material will deform under a shear force without failure.
Shear strength is the measure of a material’s ability to resist shear forces before it breaks or yields, whereas shear modulus describes how a material deforms under shear stress, even before failure occurs.
| Property | Shear Strength | Shear Modulus |
|---|---|---|
| Definition | Maximum stress before failure | Resistance to shear deformation |
| Application | Structural design, machinery | Deformation analysis, torsion |
| Focus | Material failure | Material deformation |
Shear Strength: A measure of failure
Shear strength is important in applications where materials must resist high forces without breaking. It’s essential for components like structural beams or pressure vessels where failure due to excessive shear force would be catastrophic.
Shear Modulus: A measure of deformation
Shear modulus helps engineers assess how materials will bend or twist under shear forces. This property is critical for understanding materials used in applications such as springs or vibration dampeners where deformation, rather than failure, is a key concern.
What Does Poisson’s Ratio Tell Us?
Poisson’s ratio is often used alongside shear modulus to help understand material deformation. But what exactly does it tell us?
Poisson’s ratio is the ratio of the lateral strain to the axial strain when a material is subjected to uniaxial stress. It provides insight into how much a material will expand or contract in directions perpendicular to the applied force.
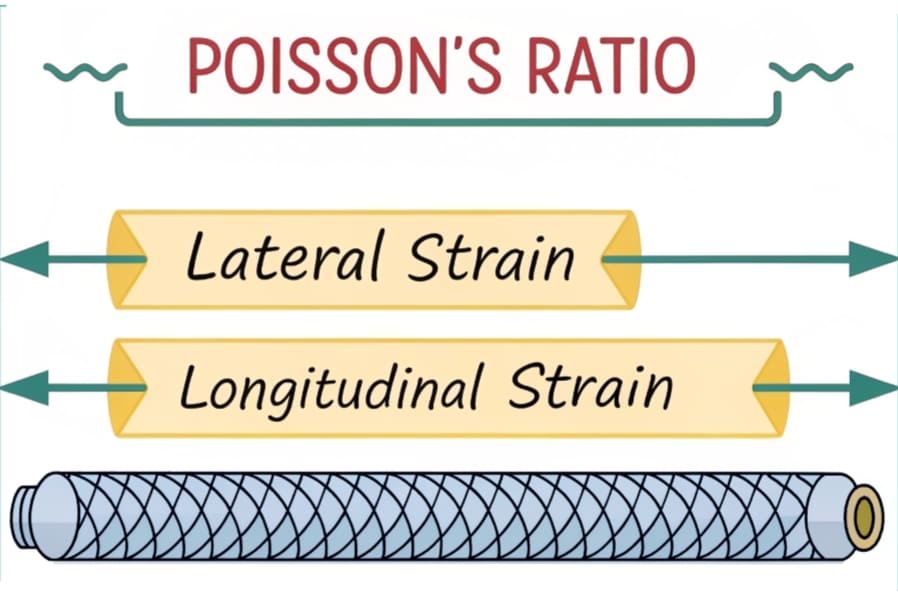
Poisson’s ratio helps complete the picture of material deformation under stress. For example, when a material is stretched in one direction, Poisson’s ratio can predict how much it will shrink in the perpendicular direction.
High vs Low Poisson’s Ratio Materials
Materials with a high Poisson’s ratio tend to shrink significantly in the perpendicular direction when stretched. For instance, metals generally have a Poisson’s ratio around 0.3, while rubber, with a higher Poisson’s ratio, contracts more when stretched. Understanding Poisson’s ratio is key when designing materials for specific mechanical applications, such as load-bearing or vibration-damping systems.
| Material | Poisson’s Ratio | Deformation Characteristics |
|---|---|---|
| Steel | 0.3 | Minimal lateral deformation under tension |
| Rubber | 0.5 | Significant lateral contraction under tension |
Why is Steel More Elastic Than Rubber?
Elasticity is the ability of a material to return to its original shape after being deformed. But why is steel considered more elastic than rubber?
Steel is more elastic than rubber because it has a higher Young’s modulus and shear modulus, meaning it resists deformation more effectively than rubber.
Steel’s atomic structure is more rigid, allowing it to return to its original shape after deformation. Rubber, on the other hand, is more flexible and can stretch a lot before returning to its original form.
The role of molecular structure
Steel is a crystalline material with tightly packed atoms, contributing to its rigidity. Rubber, made from long polymer chains, is much more flexible and can stretch easily. The differences in these structures explain why steel is more elastic than rubber, making steel ideal for structural and mechanical applications.
Why Elasticity Matters in Engineering
The high elasticity of steel makes it an ideal choice for structural applications where materials are subjected to repetitive loads. Rubber, with its flexibility, is more suitable for applications like seals and dampers where deformation is expected but failure isn’t a concern.
Is Shear Modulus Same as Tensile Modulus?
Shear modulus and tensile modulus are often confused, but they measure different aspects of material behavior. Let’s clear this up.
No, shear modulus and tensile modulus are not the same. While shear modulus measures resistance to shear stress, tensile modulus (or Young’s modulus) measures resistance to elongation or compression under tensile forces.
Tensile modulus (or Young’s modulus) describes how much a material elongates or compresses when stretched or squeezed. Shear modulus, however, is concerned with how a material deforms when subjected to twisting or shearing forces.
Differences in practical use
In engineering, tensile modulus is essential when dealing with materials that are stretched or compressed, such as cables or beams. Shear modulus, however, is crucial for applications involving twisting or shearing, like shafts and gears.
How to Determine Shear Modulus?
Determining the shear modulus of a material is essential for many engineering applications. So, how do you go about measuring it?
Shear modulus can be determined experimentally by applying a known shear force to a material and measuring the resulting deformation. The formula is shear modulus = shear stress / shear strain.

In the laboratory, a sample of the material is subjected to a shear force, and the resulting strain (deformation) is measured. The shear modulus is then calculated by dividing the shear stress by the shear strain.
Practical considerations
In real-world scenarios, shear modulus can be obtained from standardized material tests, such as torsion tests, or by using specialized testing machines that apply controlled shear forces. For complex materials like composites or polymers, specialized techniques may be required.
| Testing Method | Shear Modulus Determination | Equipment Needed |
|---|---|---|
| Torsion Test | Twist material and measure strain | Torsion testing machine |
| Dynamic Testing | Measure wave velocity changes | Ultrasonic tester |
Is Shear Modulus the Same as Bulk Modulus?
Bulk modulus and shear modulus are related to how a material deforms, but they deal with different types of stress. Are they the same?
No, shear modulus and bulk modulus are different. Shear modulus measures a material’s resistance to shear forces, while bulk modulus measures how a material compresses under uniform pressure.
Bulk modulus describes how a material responds to changes in pressure, focusing on how much it will shrink when pressure is applied. Shear modulus, on the other hand, is concerned with how the material deforms when forces act tangentially to the surface.
Why the difference matters
Both moduli are essential for understanding material behavior in different environments. Bulk modulus is more relevant in fluid mechanics and materials science, while shear modulus is crucial in situations involving shearing forces, like structural and mechanical systems.
| Property | Bulk Modulus | Shear Modulus |
|---|---|---|
| Type of Stress | Uniform Pressure | Shear (Tensile) |
| Material Behavior | Compression | Twisting/Shearing |
When to Use Shear Modulus?
Shear modulus is widely used in engineering, but when should it be specifically applied? Let’s explore its relevance in design and construction.
Shear modulus is typically used in situations where materials experience shear forces, such as in mechanical shafts, beams, and components that twist or bend.
Shear modulus is especially relevant for materials subjected to torsion or shear stress, like in machinery, structural components, and vehicle parts. It helps predict how a material will respond when subjected to forces that cause it to twist or change shape.
What is Shear Modulus Relevant For?
Shear modulus plays a key role in many industries. But what is it really relevant for, and why does it matter in material selection?
Shear modulus is crucial in engineering, construction, and materials science, particularly in applications where materials experience twisting or shear forces, such as in shafts, gears, and structural components.
Understanding shear modulus allows engineers to select the right materials for specific applications, ensuring that components will resist deformation under shear forces. This property is particularly important in aerospace, automotive, and manufacturing, where materials must withstand high shear stresses.
What is the Shear Modulus for Steel?
Steel is widely used in construction and manufacturing. But what is the shear modulus for steel, and how does it compare to other materials?
The shear modulus for steel typically ranges between 70 and 80 GPa (gigapascals), which is significantly higher than many other materials. This high value makes steel resistant to shear deformation.

Steel’s high shear modulus means it resists deformation under shear forces, making it ideal for use in structural components, machinery, and other applications requiring high strength and minimal deformation.
Steel’s performance in shear
Due to its high shear modulus, steel is particularly effective in applications involving torsion and bending, such as beams, columns, and mechanical parts like shafts. Its performance under shear stress makes it a preferred material in industries where strength and minimal deformation are essential, including construction and automotive manufacturing.
Conclusion
Shear modulus is a critical property that defines how a material behaves under shear stress. Understanding its significance helps engineers make better material choices for various applications, ensuring components are durable and resistant to deformation under the forces they will experience.
